Les arbres de Merkle dans Bitcoin
Lorsqu'on s'intéresse à comment Bitcoin fonctionne, on entend parfois parler des arbres de Merkle qui interviennent dans la validation des transactions et des blocs. Décrits par Satoshi Nakamoto dans le livre blanc, ils forment un rouage essentiel dans le fonctionnement de la cryptomonnaie. Ils sont aussi à la base d'idées diverses comme Taproot. Dans cet […]

Acheter Bitcoin (BTC)
Publicité Kraken
Lorsqu'on s'intéresse à comment Bitcoin fonctionne, on entend parfois parler des arbres de Merkle qui interviennent dans la validation des transactions et des blocs. Décrits par Satoshi Nakamoto dans le livre blanc, ils forment un rouage essentiel dans le fonctionnement de la cryptomonnaie. Ils sont aussi à la base d'idées diverses comme Taproot.
Dans cet article nous allons nous intéresser à ce que sont les arbres de Merkle et à comment ils sont utilisés dans Bitcoin.
Qu'est-ce qu'un arbre de Merkle ?
Un arbre de Merkle, ou arbre de hachage, est un concept mathématique inventé en 1979 par le cryptographe Ralph Merkle. Il s'agit d'un modèle de structure de données contenant un résumé d'information d'un volume de données, généralement grand.
Les arbres de Merkle se basent sur une fonction de hachage. Comme on le sait, les fonctions de hachage, comme SHA-256 par exemple, ont pour propriété de prendre en entrée une donnée de taille arbitraire et de lui donner une empreinte de taille fixe à partir de laquelle il est impossible de retrouver la donnée initiale. Il s'agit donc de fonction à sens unique : il faut connaître le message original pour le lier à son empreinte.
Dans un arbre de Merkle, les données (appelées feuilles) sont rangées dans un certain ordre et sont toutes hachées. Puis leurs empreintes sont combinées deux à deux pour être hachées à leur tour, et ceci jusqu'à ce qu'il ne reste plus qu'une seule empreinte, qu'on appelle la racine.
Étudions un exemple d'arbre de Merkle basé sur 6 données différentes : DA, DB, DC, DD, DE et DF.
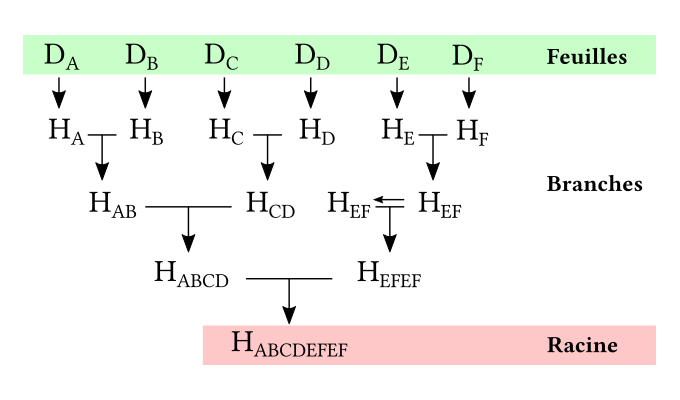
Les données sont hachées par la fonction de hachage notée h. Pour la donnée DA, on calcule :
HA = h( DA )
Puis leurs empreintes sont concaténées deux à deux : la deuxième empreinte est mise à la suite de la première pour qu'elles soient hachées ensemble. De cette manière les empreintes des données DA et DB permettent de calculer l'empreinte HAB :
HAB = h( HA + HB )
On réitère ensuite le processus. Dans le cas où le nombre d'empreintes à combiner est impair, on combine la dernière empreinte avec elle-même : ainsi, dans notre exemple, on doit concaténer HEF avec elle-même pour calculer HEFEF :
HEFEF = h( HEF + HEF )
Enfin, une fois qu'il ne reste qu'une seule empreinte, l'arbre est complet et l'empreinte obtenue est appelée racine de Merkle.
Dans un arbre de Merkle, démontrer qu'une feuille fait partie de l'arbre requiert de calculer un nombre d'empreintes proportionnel au logarithme du nombre de feuilles (log(n)), et non pas proportionnel au nombre de feuilles lui-même (n) comme ce serait le cas dans une structure « naïve ».
Cela fait que les arbres de Merkle sont utiles pour agencer un grand nombre de données. Et c'est notamment pour cette raison qu'ils sont utilisés dans des systèmes logiciels comme Git ou BitTorrent, ainsi que, vous l'avez deviné, dans Bitcoin.
Bitcoin et la vérification de paiement simplifiée
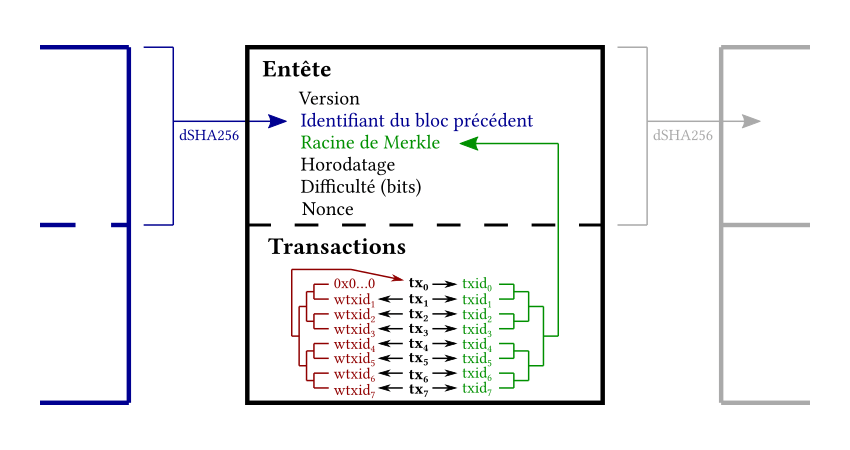
Dans Bitcoin, les arbres de Merkle sont utilisés pour agencer les transactions au sein des blocs. À chaque nouveau bloc, un arbre de Merkle est construit par le mineur et la racine calculée est placée dans l'entête de ce bloc. Par exemple, on va retrouver la racine de Merkle b191f5f973b9040e81c4f75f99c7e43c92010ba8654718e3dd1a4800851d300d dans l'entête du bloc 630 000 de Bitcoin, qui est un résumé des 3134 transactions qu'il contient.
La fonction de hachage utilisée pour construire l'arbre de Merkle est le double SHA-256, fonction qui sert également à lier les blocs entre eux et à calculer l'identifiant des transactions pour les répertorier plus facilement. Cela veut dire que les premières empreintes de l'arbre seront aussi les identifiants des transactions, et qu'il ne sera pas nécessaire de les calculer plusieurs fois.
La racine calculée est toujours placée dans l'entête du bloc.
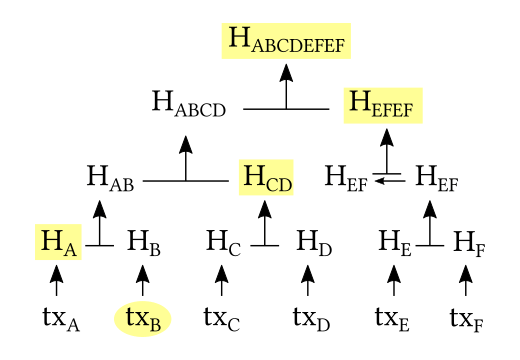
Cet arrangement des transactions dans un arbre de Merkle permet une chose importante pour les portefeuilles légers dans Bitcoin : il s'agit de la vérification de paiement simplifiée, ou Simplified Payment Verification (SPV) en anglais, décrite par Satoshi Nakamoto dans la section 8 du livre blanc.
Les portefeuilles légers sont les logiciels qui ne téléchargent que les entêtes des blocs et non l'intégralité des blocs de la chaîne. Pour vérifier une transaction, il leur suffit donc de récupérer la branche de Merkle qui correspond à leur transaction (pour la transaction txB dans notre exemple ci-dessus, il s'agira des empreintes HA, HCD et HEFEF) de manière à recalculer la racine et à la comparer avec celle contenue dans l'entête.
Ainsi les portefeuilles légers comme BRD ou Neutrino n'ont pas besoin de télécharger l'entièreté du bloc pour vérifier que leur transaction a bien été incluse dans ce bloc.
Depuis l'activation de SegWit le 24 août 2017, chaque bloc est constitué de deux arbres de Merkle : l'arbre des transactions classiques décrit ici, et l'arbre des témoins (qui est l'arbre des transactions incluant les signatures des transactions SegWit). La racine de l'arbre des témoins est placée dans la transaction de récompense du bloc, de sorte que la racine de Merkle principale dépende d'elle.
Notez que Bitcoin n'est pas le seul à utiliser les arbres de Merkle et beaucoup d'autres protocoles crypto-économiques s'en servent pour structurer les transactions dans les blocs. Par exemple, Ethereum fait usage de trois arbres de Merkle (des arbres de Merkle-Patricia modifiés pour être précis) pour agencer trois types de données : les transactions, les reçus (receipts), qui sont des données montrant l'effet des transactions, et les données relatives à l'état du système (soldes et nonces des comptes, code des contrats, données inscrites sur la chaîne).
Il est également prévu que Bitcoin Cash fasse une transition vers un arbre dit « de Meklix » afin de partitionner la validation des blocs en vue d'un meilleur passage à l'échelle.
Les arbres syntaxiques abstraits merkélisés (MAST)
Un autre usage que l'on peut trouver aux arbres de Merkle est la structuration des contrats autonomes, usage qui apporte des avantages en matière de scalabilité et de confidentialité. Les arbres utilisés de cette façon sont appelés arbres syntaxiques abstraits merkélisés ou Merklized Abstract Syntax Trees en anglais, et son souvent abrégés en MAST.
Essentiellement, il s'agit de scinder les différentes conditions d'un contrat et de les agencer dans un arbre de Merkle ou une structure semblable.
Par exemple, prenons un contrat dont les trois conditions de dépense sont :
- Ou bien Alice et Bob fournissent leurs signatures :
2 <clé publique d'Alice> <clé publique de Bob> 2 CHECKMULTISIG
- Ou bien Carole signe 30 jours après que les fonds ont été déposés :
<temps de verrouillage : 30 jours> CHECKSEQUENCEVERIFY DROP <clé publique de Carole> CHECKSIG
- Ou bien Damien signe après 2050 :
<verrouillage jusqu'en 2050> CHECKLOCKTIMEVERIFY DROP <clé publique de Damien> CHECKSIG
On peut alors intégrer le contrat sous la forme d'un arbre de Mekle.
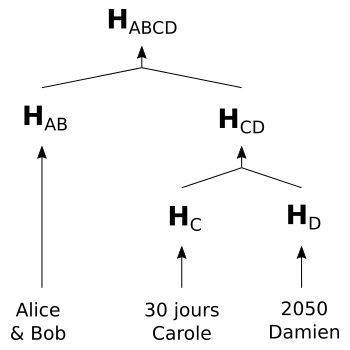
Dans ce cas, il est possible pour les participants d'exécuter une condition du contrat sans révéler les autres conditions. Au moment de l'exécution, un participant fournira sa condition ainsi que la branche de Merkle correspondante. Le réseau n'aura ainsi qu'à vérifier que le calcul de l'arbre correspond bien à la racine stockée sur la chaîne (qui sert d'adresse au contrat).
Il n'est pas prévu que les MAST soient implémentés dans Bitcoin le moment. Néanmoins, une version améliorée de cette structure, appelée Taproot, devrait voir le jour prochainement avec la version 1 de SegWit, ajoutant les signatures de Schnorr. Il y existe également d'autres variantes de la même idée comme Graftroot ou G'root.
? Pour savoir plus sur Taproot, je vous recommande de lire : Taproot : des smart contracts confidentiels pour Bitcoin