Portefeuille, phrase secrète et génération d'adresses

Quand vous utilisez un portefeuille pour la première fois, le programme vous incite à recopier une phrase de récupération composée de 12 ou 24 mots provenant de l'anglais, du français ou d'une autre langue. Cette phrase sert à retrouver vos fonds en cas de casse ou de vol : c'est pourquoi elle doit rester secrète. Comment cette récupération fonctionne-t-elle ? C'est ce que nous allons découvrir ici.
Qu'est-ce qu'une phrase secrète exactement ?
En fait, dans la plupart des portefeuilles modernes, les clés privées et les adresses ne sont pas générées aléatoirement, mais sont plutôt dérivées de façon déterministe à partir de cette phrase secrète. Cette phrase mnémotechnique est donc l'unique information que l'utilisateur ne doit pas perdre. Cela s'avère très pratique puisque les portefeuilles génèrent une nouvelle adresse à chaque paiement réalisé et sont amenés à gérer un grand nombre de clés privées.
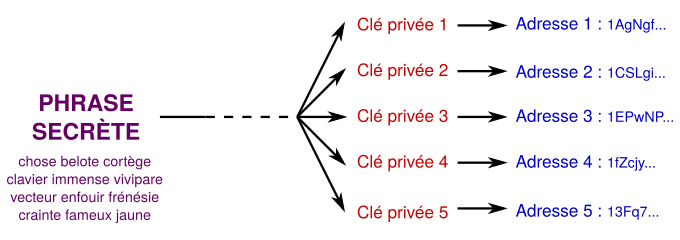
Ce type de portefeuille est parfois appelé HD wallet pour Hierarchical Deterministic Wallet. Ce standard a été développé pour Bitcoin à partir de 2012 et est décrit dans les propositions BIP-32, BIP-39 et BIP-44. En outre, il est utilisé par tous les systèmes de cryptomonnaie comme Ethereum, Bitcoin Cash, Litecoin, Monero, Dash, etc.
Si les notions de clé privée et d'adresse vous échappent, nous vous recommandons chaudement de consulter notre article « Clés privées, clés publiques et adresses dans Bitcoin » avant de poursuivre la lecture de cet article.
Comment la phrase secrète est-elle créée ?
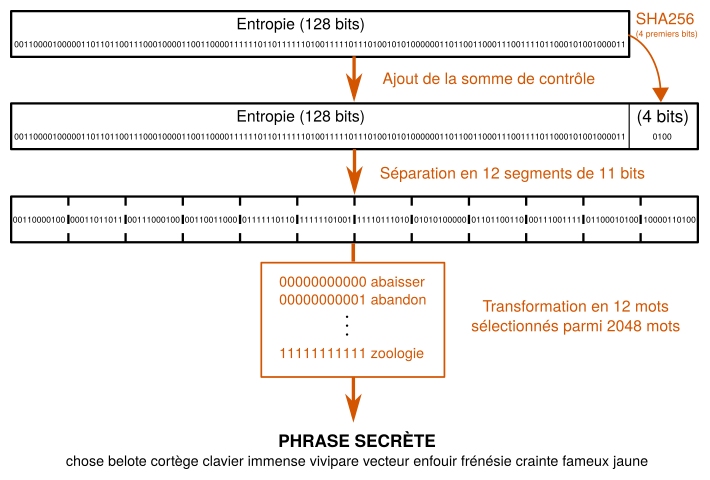
La phrase secrète, ou phrase de récupération, est générée aléatoirement par le portefeuille. Qu'il s'agisse d'un smartphone, d'un ordinateur ou d'un portefeuille matériel, l'appareil crée une suite de bits choisis au hasard appelée entropie grâce à des procédés cryptographiquement fiables.
Dans le cas des phrases secrètes des adresses Bitcoin (et de beaucoup d'autres crypto-actifs), cette entropie est enrichie d'une somme de contrôle de quelques bits qui permettra de détecter les erreurs dans la phrase. Elle est ensuite divisée en segments de 11 bits. Enfin, chacun de ces segments est associé à un mot dans la liste standard de 2048 mots, ce qui permet de former la phrase.
Le nombre de bits de l'entropie et de la somme de contrôle dépendent du nombre de mots que l'on désire : pour 12 mots, on aura une entropie de 128 bits et une somme de contrôle de 4 bits ; pour 24 mots, on aura une entropie de 256 bits et une somme de contrôle de 8 bits. Il est possible d'avoir 12, 15, 18, 21 ou 24 mots par phrase, à l'heure actuelle.
Comment la phrase secrète est-elle utilisée ?
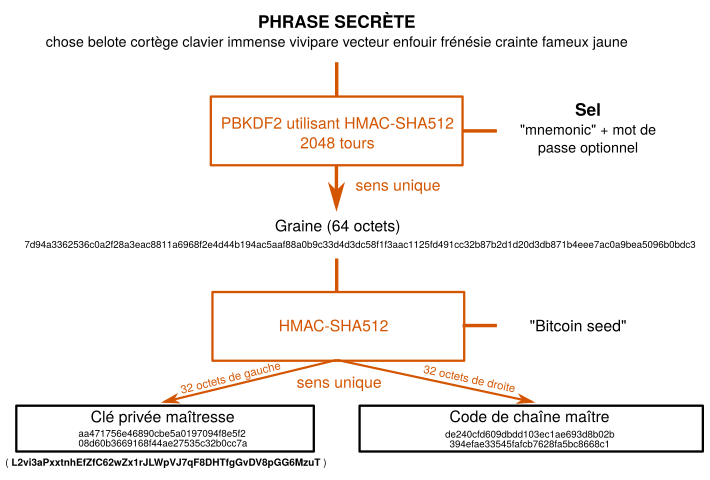
Une fois que la phrase secrète est générée, divers procédés de hachage sont appliqués pour dériver les clés. Elle est passée par la fonction de dérivation de clés PBKDF2 (Password-Based Key Derivation Function 2) qui applique la fonction HMAC-SHA512 (HMAC pour hash-based message authentication code) de manière répétée : ici 2048 tours. L'information obtenue est appelée graine. Au-delà des noms barbares employés, il faut savoir que cette méthode a pour intérêt de rajouter beaucoup de temps de calcul, ce qui complique le cassage de la graine (et de toutes les clés dérivées) par la force brute. De plus, un sel cryptographique est utilisé pour renforcer la sécurité du processus.
⚠ Le nom de graine est parfois attribué à la phrase mnémotechnique elle-même.
On réutilise ensuite la fonction HMAC-SHA512 pour obtenir la clé privée maîtresse et le code de chaîne maître à partir de la graine. Ces deux informations nous permettront de dériver par la suite toutes les autres clés ainsi que les adresses.
Comment sont dérivées les clés privées et les adresses ?
Comme expliqué ci-dessus, nous pouvons dériver une clé privée maîtresse de la phrase secrète. Mais cette dernière n'est pas la seul élément qui en ressort : il y a également un code de chaîne qui est créé. Ce code de chaîne intervient dans la chaîne de dérivation des clés, de sorte qu'il soit impossible de procéder à la dérivation sans lui.
Plutôt que de devoir gérer ces deux informations, on préfère les regrouper dans une unique chaîne de caractère appelée clé privée étendue (extended private key). Cette chaîne de caractère commence toujours par xprv. La clé privée étendue issue de la clé privée maîtresse et du code de chaîne maître est, dans notre cas :
xprv9s21ZrQH143K4GddX63HehNqE3mywQEgBkdxWcw83mimQj2d4FtwEjjBfnAroK1noMPgT3wLxE32wv2dKaj7m3dMrma76BeJzx24FUok1z5
On définit de la même façon une clé publique étendue qui regroupe simplement la clé publique correspondant à la clé privée et le code de chaîne. Cette clé commence toujours par xpub. La clé publique étendue correspondant à la clé privée précédente est :
xpub661MyMwAqRbcGki6d7aJ1qKZn5cULrxXYyZZK1Ljc7FkHXMmboDBnY3fX51XDPjeiJQjDBzk9LJDoBaB2djbKGGt8ezAFHjtYAx2352kReW
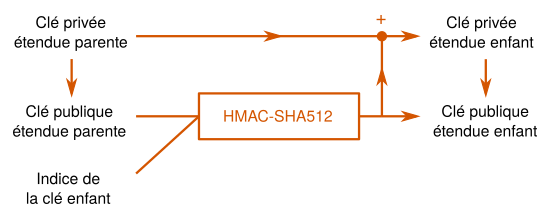
La dérivation des clés (child key derivation) consiste à utiliser l'algorithme HMAC-SHA512 pour dériver des clés étendues « enfant » à partir d'une clé parente. Le premier type de dérivation, la dérivation normale, fait intervenir la clé publique étendue dans le processus, ce qui rend possible deux opérations distinctes :
- L'obtention d'une clé privée étendue à partir de la clé privée parente : le résultat du hachage par le HMAC est additionné à la clé privée parente.
- L'obtention d'une clé publique étendue à partir d'une clé publique parente. La clé publique résultante correspond bien évidemment à la clé privée ci-dessus.
Cette particularité de la dérivation se révèle extrêmement utile lorsqu'on veut générer de nouvelles adresses sans compromettre la clé privée racine. Ainsi, un commerçant pourrait par exemple donner une clé publique étendue à ses employés pour qu'ils puissent recevoir des paiements à différentes adresses sans avoir à leur révéler la clé privée correspondante.
Il existe également un second type de dérivation, la dérivation endurcie (hardened derivation), qui permet de se restreindre à la dérivation des clés privées étendues en ne faisant intervenir que la clé privée.
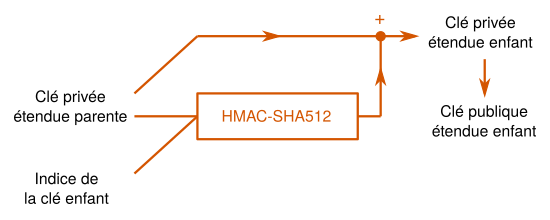
Notez qu'on peut dériver un grand nombre de clés à partir d'une clé unique. Chaque clé est munie d'un indice qui est utilisé dans la dérivation. Cet indice peut aller de 0 à 2 147 483 647. Ainsi, la première clé sera la clé 0, le seconde la clé 1, etc. L'usage veut qu'on utilise une apostrophe lorsqu'on parle de dérivation endurcie et qu'on n'en utilise pas lorsqu'on parle de dérivation normale. Ainsi, la clé d'indice 0 dérivée normalement sera notée 0, et la clé d'indice 2 dérivée de manière endurcie sera notée 2'.
Le fonctionnement standard des portefeuilles
Cette dérivation des clés est utilisée par tous les portefeuilles modernes. Pour ce faire, le portefeuille utilise un chemin de dérivation qui désigne les dérivations successives nécessaires pour obtenir les clés qui servent effectivement à créer les adresses. Ce chemin de dérivation peut varier selon les portefeuilles, mais le standard le plus répandu est celui qui est défini dans le BIP-44.
La clé privée maîtresse (notée m) est dérivée plusieurs fois de manière endurcie. Tout d'abord, la dérivation utilise l'indice 44 : celui-ci indique le but visé (ici la construction d'un portefeuille déterministe selon le BIP-44). Puis on dérive cette clé avec un indice indiquant l'identifiant du protocole : le 0 indique Bitcoin, le 60 Ethereum, le 145 Bitcoin Cash, etc. On a enfin recours à une autre dérivation pour obtenir la clé correspondante au compte, ce standard autorisant la possibilité de créer plusieurs comptes à partir d'une même graine. La plupart du temps on n'utilise que le compte numéro 0 comme ici. Le chemin de dérivation est donc m/44'/0'/0'.

Une fois que la clé du compte a été calculée, le portefeuille va procéder à des dérivations normales pour obtenir les clés et les adresses utilisées pour transférer des fonds. Ce faisant il va construire deux branches : l'une associé à l'indice 0, celle des adresses externes, censées être partagées publiquement pour recevoir des fonds ; l'autre associée à l'indice 1, celle des adresses internes, utilisées pour « rendre la monnaie » lors des paiements.
De cette manière, la première adresse de réception que vous devriez voir sera celle qui sera associée à la clé m/44'/0'/0'/0/0. Le portefeuille se chargera ensuite de générer une autre adresse lorsqu'elle aura été utilisée. Notez cependant que la première adresse reste valide et peut recevoir des fonds tant que vous avez accès à votre portefeuille.
Conclusion
Vous l'avez constaté : tout le processus est standardisé pour qu'il soit possible de récupérer l'intégralité des fonds en cas de casse, de perte ou de vol de l'appareil contenant les clés. Tout cela est défini pour Bitcoin, mais aussi pour l'intégralité des monnaies numériques de la cryptosphère, ce qui facilite grandement le fonctionnement des portefeuilles multi-monnaies.
Si vous voulez vous amuser à observer ce que donne la dérivation d'une phrase secrète précise, vous pouvez vous rendre sur le site suivant : https://iancoleman.io/bip39/. Faites néanmoins attention à ne pas révéler la phrase de votre vrai portefeuille, même si le site semble digne de confiance.
? Et si la société qui m'a fourni mon cold wallet disparaît ?
Note de l'article













J’ai perdu ma phrase secrète. Est il possible de la retrouver avec l'adresse mail de portefeuille?
Non ce n'est pas possible si vous n'avez pas noté, ou enregistré, les 12 ou 24 mots quelques part, désolé.
J’ai perdu ma phrase secrète. Est il possible de la retrouver ?
Malheureusement non sauf si vous l'avez noté ou enregistré quelque part.