La programmation avec Bitcoin : Les courbes elliptiques

Aujourd'hui nous allons rentrer dans la technique autour de Bitcoin. Avant de pouvoir mettre nos mains dans la programmation Bitcoin, il faut bien comprendre certaines notions. C'est pour cela que je vais vous présenter les courbes elliptiques et leur utilisation au sein de Bitcoin. Les non-mathématiciens peuvent se rassurer : je n'en suis pas un moi-même, et resterai le plus simple possible dans ces explications. Ce n'est pas une notion mathématiquement très complexe, et des souvenirs de cours de lycée suffisent pour se remettre dans le bain. Pas de code dans cet article, découvrons ensemble le monde des courbes elliptiques !

Ce qu'est une courbe elliptique

Avant de se lancer dans les courbes elliptiques, il est pertinent de se remémorer ce qu'est une courbe en mathématique. Une courbe est une représentation graphique qui décrit certaines relations ou fonctions d'une figure géométrique quelconque. Bon ça ne nous avance pas vraiment, mais voici quelques exemples de courbes connues pour se rafraîchir la mémoire.

Voici un exemple de courbe linéaire :

y = a x + b

Et sa version graphique :

Voici un exemple de courbe quadratique :

y = a x2 + b x + c

Dont on peut voir la version graphique ci-dessous :

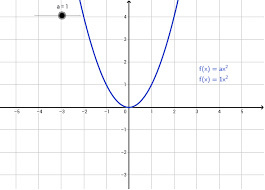
On observe donc l'évolution des résultats de l'équation en fonction des paramètres que l'on utilise.

Une courbe elliptique est un cas particulier de courbe, qui possède des propriétés intéressantes. Rien à voir avec les ellipses, elles permettent de réaliser des additions de points sur leurs tracés. C'est pour ces raisons qu'elles sont utilisées dans plusieurs domaines et notamment ce qui nous intéresse, la cryptographie.

Voici mathématiquement à quoi ressemble une courbe elliptique :

y2 = x3 + a x + b

Et voici ses versions graphiques :

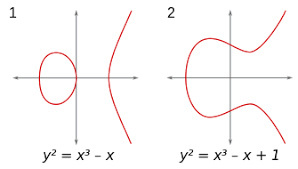
On comprend donc bien qu'il n'y a pas de rapport avec les ellipses.

Les courbes elliptiques et Bitcoin

Bitcoin utilise la courbe elliptique pour beaucoup d'usages, principalement dans le cadre de la gestion des clés publique et privée. La création d'un nouveau compte Bitcoin, et donc sa clé publique se fait par une addition elliptique. Mais c'est également sur quoi se repose Bitcoin pour garantir que l'utilisateur transférant des bitcoins en est le véritable propriétaire. On retrouve donc plusieurs termes connus de l'utilisation de Bitcoin qui utilisent des algorithmes liés à une courbe elliptique :

• La clé privée d'un utilisateur. La clé privée d'un utilisateur n'est théoriquement connue que de lui-même. C'est un nombre choisi complètement aléatoirement, utilisant un algorithme de génération aléatoire sécurisé.
• La clé publique de ce dernier. C'est un nombre dérivé d'une clé privée, mais qui peut être rendu public pour les autres utilisateurs. Il est conseillé de ne pas réutiliser les clés publiques. Je vous décris l'opération plus en détail par la suite, mais l'idée reste simple. Il est très simple de créer une clé publique depuis une clé privée, mais l'opération inverse relève de l'impossible.
• Les signatures de transactions. Les signatures permettent aux utilisateurs de valider une transaction avant de l'envoyer sur le réseau. Elles sont composées d'un hash de la transaction ainsi que de la clé publique. Avec la signature et la clé publique, il est possible de déterminer s'il s'agit bien du propriétaire des fonds qui réalise le transfert. Nous verrons les détails techniques de ce principe par la suite.
• La courbe elliptique secp256k1.

Il existe de nombreuses courbes elliptiques, qui utilisent des paramètres différents. Celle qu'utilise Bitcoin est assez méconnue puisqu'il ne s'agit pas du standard recommandé. Il s'agit de secp256k1, qui a gagné en popularité en même temps que Bitcoin. Elle présente des avantages liés à l'efficacité, puisque ses paramètres sont très petits et permettent des calculs plus rapides. Si vous vous souvenez, l'équation d'une courbe elliptique ressemble à cela :

y2 = x3 + a x + b

Eh bien les paramètres de secp256k1 étant respectivement a = 0 et b = 7, son équation est donc :

y2 = x3 + 7

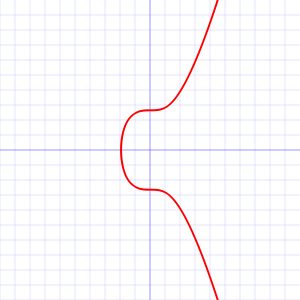
Vous pouvez retrouver les spécificités de la courbe secp256k1 de manière plus détaillée juste ici. Vous retrouverez également une liste d'autres courbes elliptiques standardisées.

L'algorithme ECDSA et son fonctionnement technique

La signature des transactions et la génération des clés privées utilisent l'algorithme ECDSA (Elliptic Curve Digital Signature Algorithm). Ce dernier est un algorithme cryptographique, reconnu comme sûr et désormais une norme dans ce domaine. Il utilise l'équation d'une courbe elliptique que nous avons vu auparavant, ayant pour paramètre des nombres entiers, dans un ensemble fini de points.

Génération des clés d'un utilisateur

Afin d'obtenir la clé privée d'un compte Bitcoin, et des clés publiques de ce dernier on utilise un système de génération de nombres aléatoires. Il s'agit pour Bitcoin du CSPRNG (cryptographically secure pseudo-random number generator). Il est donc théoriquement impossible de déterminer une clé privée sans information, même en ayant recours à du brute force (principe de réaliser de multiples tentatives les unes après les autres). Vous pouvez même vous générer votre propre clé privée, mais attention aux algorithmes utilisés ! S'ils ne sont pas suffisamment sécurisés, utilisant des système de seed par exemple, d'autres utilisateurs pourraient la retrouver.

Mais pas besoin de courbe elliptique pour le moment, quand est-elle utilisée ? Eh bien si la génération des clés privée se fait sans secp256k1, celle des clés publique l'utilise. Une clé publique est le résultat d'une multiplication de la clé privé et du point générateur. Ce point générateur est le même pour tout les utilisateurs de Bitcoin. Ce procédé est très intéressant puisque si réaliser une multiplication est très simple, retrouver la clé privée est impossible. En effet l'algorithme des courbes elliptiques, en utilisant les paramètres de secp256k1 est une fonction dite « one-way ». La formule est la suivante :

K = k * G

K représente la clé privée de l'utilisateur, k est la clé publique de ce dernier. Enfin G est une constante, le fameux point générateur.

La sécurité de secp256k1

En cryptographie, les différents algorithmes rendus publics doivent montrer patte blanche pour être accepté par la communauté. En effet leurs auteurs pourraient avoir mis en place des backdoors à leur création : cela signifie qu'en utilisant des paramètres précis, ces derniers pourraient accéder à des fonctions théoriquement impossibles, dans notre cas retrouver une clé privée à partir d'une clé publique. C'est pour cela que les créateurs doivent présenter leurs choix et les justifier, l'algorithme ainsi que les paramètres fixés.

Dans le cas de Bitcoin, ce sont les paramètres a et b ainsi que le point générateur. En ce qui concerne les paramètres respectivement 0 et 7, on comprend l'intérêt dans le cadre de l'optimisation et les chiffres sont vraiment petits pour être des backdoors. Pour le point générateur, le choix est souvent aléatoire. Ce n'est pas Satoshi qui l'a défini, c'est un des paramètres inhérents à la courbe secp256k1.

La courbe elliptique pour le développeur Bitcoin

On a donc vu ce qu'était une courbe elliptique et comment le protocole Bitcoin en tirait parti pour assurer une sécurité au niveau du stockage et des échanges des bitcoins. Mais en tant qu'apprenti développeur ou développeur Bitcoin, pourquoi est-ce important ?

Tout d'abord il est nécessaire de comprendre les principes avant de se mettre à coder des lignes sans comprendre l'ensemble. Les courbes elliptiques sont très accessibles, et leur place dans le protocole en font des notions intéressantes à apprendre. Mais ce n'est pas la seule raison si vous souhaitez travailler sur Bitcoin. Les courbes elliptiques sont au cœur de la réalisation des transactions, puisque la signature d'une transaction est liée à secp256k1. En effet la signature d'une transaction, qui permet de garantir que les bitcoins transférer sont les nôtres, utilise la courbe elliptique. De plus, comme on l'a dit, la génération de clés Bitcoin repose également sur secp256k1.

Développement d'un wallet Bitcoin

Donc si vous souhaitez développer par exemple un wallet Bitcoin, il vous faudra maîtriser ces calculs. En effet la génération de clés Bitcoin doit se faire pour des raisons de sécurité sur le client final. Même si dans l'open source il est aisé de trouver du code fonctionnel, il est compliqué de l'implémenter sans le comprendre. Si vous voulez également permettre à vos utilisateurs de réaliser des transactions, ils leurs faudra pouvoir les signer. La courbe elliptique rentre donc encore une fois en jeu. C'est pour ces principales raisons que les programmes de formation au développement Bitcoin intègrent très rapidement des chapitres sur les courbes elliptiques. Et pour cela qu'en tant que développeur Bitcoin il vous faut passer par cette étape. Cela étant dit, à la lecture de cet article vous possédez désormais les notions de base.

Voilà pour cette explication de ce que sont les courbes elliptiques, et quelles sont leurs liens avec Bitcoin. Les courbes elliptiques permettent donc une fonctionnalité majeure dans ce dernier. Il s'agit de permettre à un utilisateur de prouver qu'il est bien le propriétaire de ses bitcoins, sans avoir à révéler sa clé privée. Cette notion peut être compliquée à digérer si les mathématiques sont derrière nous, mais cela reste relativement simple et illustré pour s'y intéresser. Connaissiez-vous l'existence de secp256k1 avant cette lecture ? N'hésitez pas à réagir à cet article dans les commentaires, ou sur Twitter.

Passionné par les crypto-monnaies, j’ai rapidement appris à développer des outils dans le domaine des technologies blockchain. J’aime partager mes connaissances sur le sujet et je participe activement au rayonnement des aspects techniques de la blockchain au sein de la communauté crypto. Je suis principalement intéressé par Ethereum et par son code Solidity.

Guillaume Chanut

62 articles

Tous ses articles